Adaptive Online Optimization of Alarm Thresholds using Multilayer Bayesian Networks and Active Transfer Entropy

Abstract

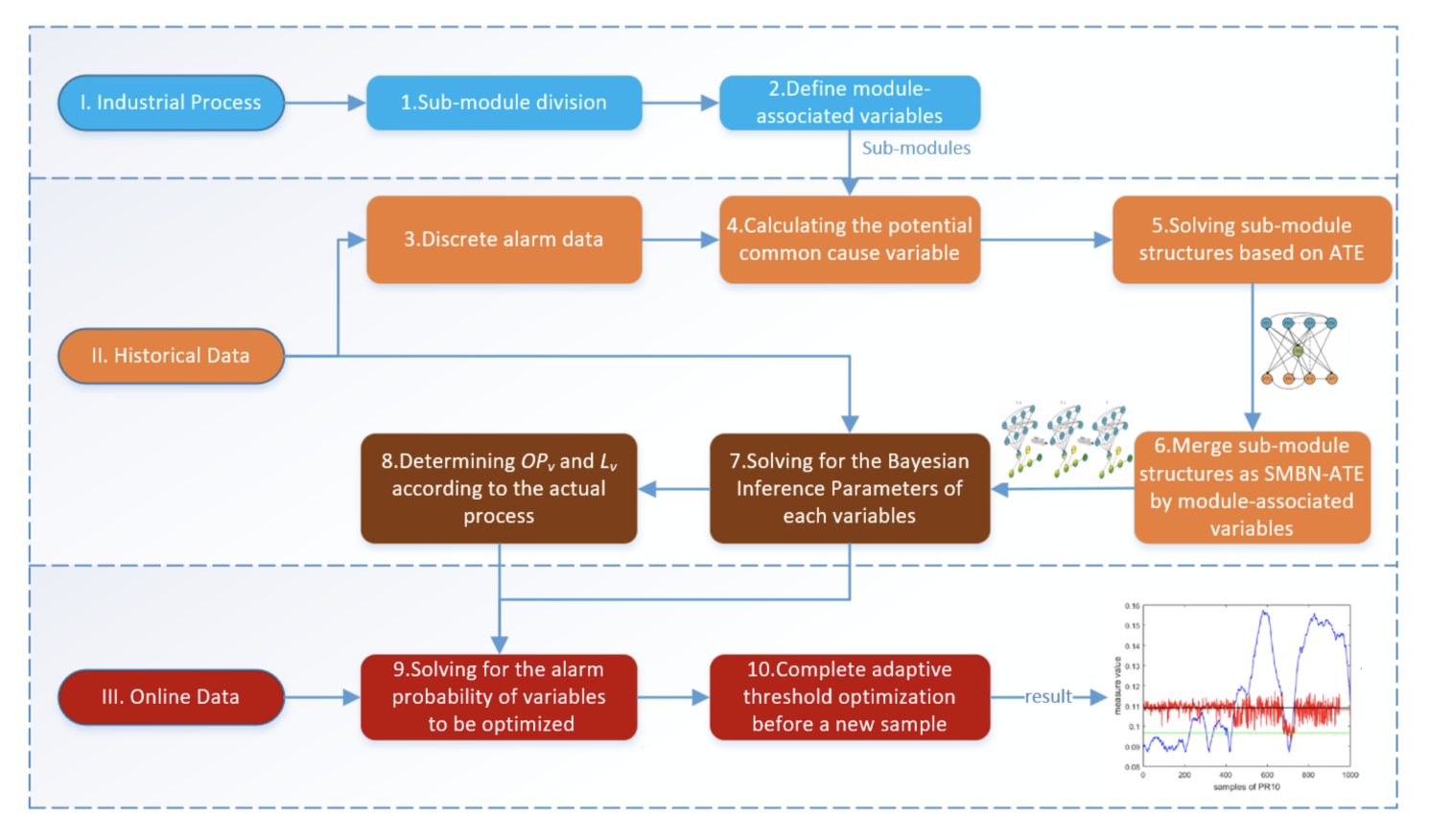
Poorly designed alarm thresholds usually lead to significant safety hazards and highly connected industrial processes. Due to the process condition changes, the traditional alarm threshold optimization methods based on historical alarm data lack the ability to adapt the thresholds online, which increases the safety risks for a given process. This paper proposes a Simplified Multilayers Bayesian Network based on Active Transfer Entropy (SMBN-ATE) to achieve adaptive online optimization of alarm threshold. Through SMBN-ATE, an accurate and streamlined alarm propagation network is constructed and then applied to predict the probability of future alarms, optimizing the alarm thresholds at each sample time. Our method has two primary advantages: (1) The constructed alarm propagation network circumvents the false causality problem caused by strong correlation and thus improves the accuracy of the alarm propagation structure. (2) The adaptive online threshold optimization adjusts threshold value in real-time based on the alarming probability and independently optimizes false and missed alarm rates. The experimental results for the micro-seismic data obtained from an actual coal mine indicate the reliability of establishing variable relationships based on Active Transfer Entropy (ATE). Furthermore, the SMBN-ATE shows high effectiveness in the Tennessee Eastman Process (TEP). Consequently, SMBN-ATE optimized the sum of the average false alarm and missing alarm rates for 16 variables from 28.5% and 27.2% to 19.7%, where 28.5% and 27.2% were calculated by the Univariate threshold setting (Uni) and False Alarm Probability and Missing Alarm Probability (FAP-MAP), respectively. It demonstrated the SMBN-ATE method to be remarkably valuable.

Read or Download: PDF