Deep Hankel matrices with random elements

Abstract

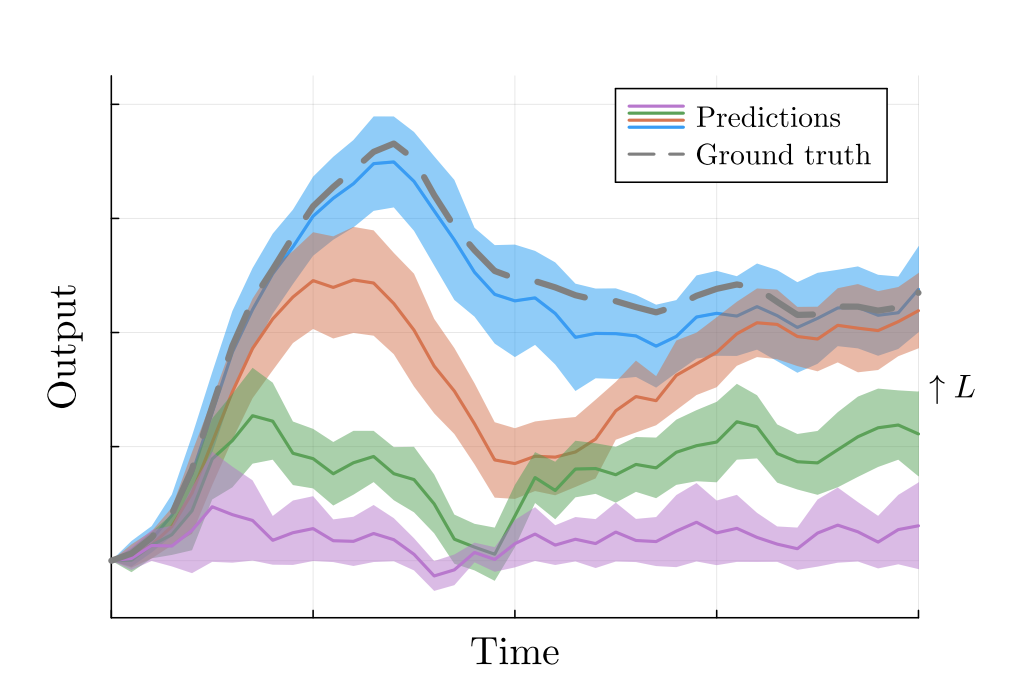
Willems’ fundamental lemma enables a trajectory-based characterization of linear systems through data-based Hankel matrices. However, in the presence of measurement noise, we ask: Is this noisy Hankel-based model expressive enough to re-identify itself? In other words, we study the output prediction accuracy from recursively applying the same persistently exciting input sequence to the model. We find an asymptotic connection to this self-consistency question in terms of the amount of data. More importantly, we also connect this question to the depth (number of rows) of the Hankel model, showing the simple act of reconfiguring a finite dataset significantly improves accuracy. We apply these insights to find a parsimonious depth for LQR problems over the trajectory space.

Read or Download: PDF