Stabilizing reinforcement learning control: A modular framework for optimizing over all stable behavior

Abstract

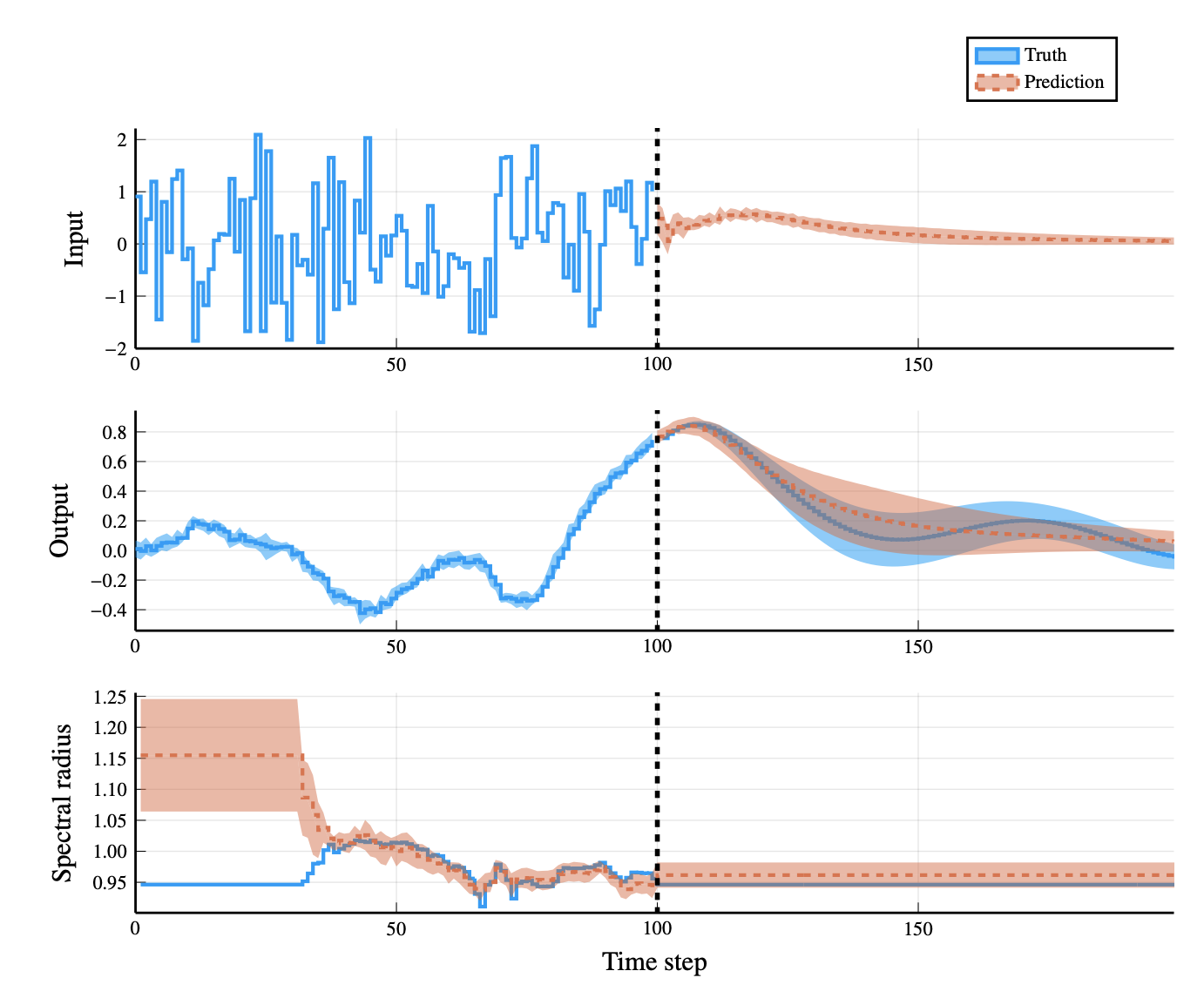
We propose a framework for the design of feedback controllers that combines the optimization-driven and model-free advantages of deep reinforcement learning with the stability guarantees provided by using the Youla-Kucera parameterization to define the search domain. Recent advances in behavioral systems allow us to construct a data-driven internal model; this enables an alternative realization of the Youla-Kucera parameterization based entirely on input-output exploration data. Perhaps of independent interest, we formulate and analyze the stability of such data-driven models in the presence of noise. The Youla-Kucera approach requires a stable 'parameter' for controller design. For the training of reinforcement learning agents, the set of all stable linear operators is given explicitly through a matrix factorization approach. Moreover, a nonlinear extension is given using a neural network to express a parameterized set of stable operators, which enables seamless integration with standard deep learning libraries. Finally, we show how these ideas can also be applied to tune fixed-structure controllers.

Read or Download: PDF